Alternative lockdowns
The flexibility of metawards means that there are multiple different
ways you could choose to model a lockdown.
To understand how, we must look at how metawards calculates the
force of infection (FOI) of each ward. The FOI of a ward is used
to calculate the infection rate, which determines the rate by which
individuals in a ward become infected.
Force of infection
The force of infection (FOI) is calculated for each ward individually, using the equation;
\(F(w) = S \times U(t) \times \sum_s [ C_s \beta_s N_s(w) ]\)
where;
\(F(w)\) is the force of infection, \(F\), calculated for a specific ward, \(w\),
\(S\) is a constant scaling parameter, set via
Population.scale_uv,\(U(t)\) is a seasonal scaling function (UV) calculated for the specified day \(t\),
\(\sum_s\) is the sum over all disease stages, \(s\),
\(C_s\) is the
contrib_foidisease parameter for stage \(s\),\(\beta_s\) is the
betadisease parameter for stage \(s\), and\(N_s(w)\) is the number of infected individuals in ward \(w\) in disease stage \(s\).
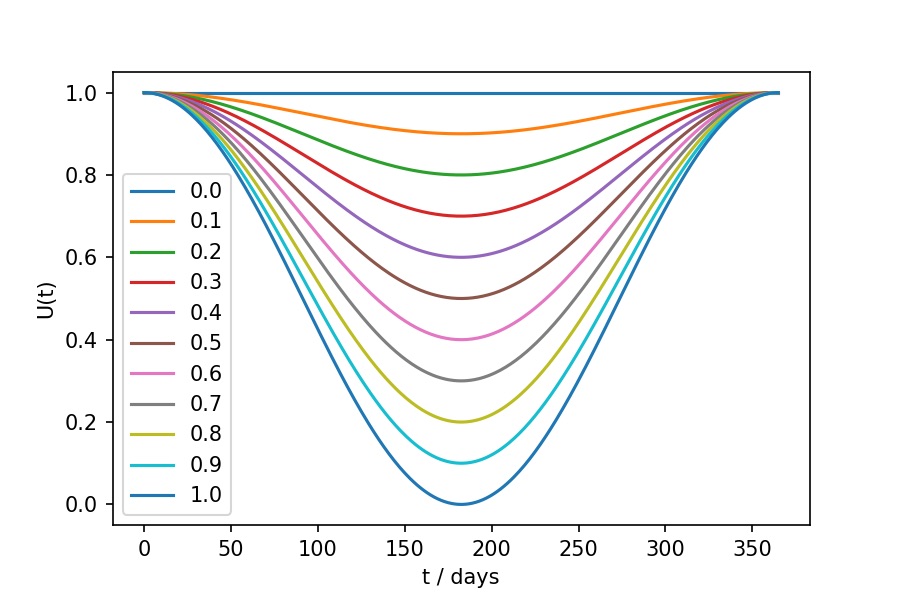
The seasonal scaling function, \(U(t)\) is calculated via;
\(U(t) = 1.0 - \frac{U_v}{2.0} + U_v \frac{\text{cos}(2 \pi t / 365)}{2.0}\)
where;
\(U_v\) is the
UVparameter supplied by the user--UVcommand line argument, and\(t\) is the number of days between the current date of the model run and the date at which seasonal spread is at a maximum,
UV_max, set via the user--UV-maxcommand line argument.
The seasonal scaling function acts to scale down the force of infection from a seasonal maximum (typically 1st January to model winter diseases in the northern hemisphere) to a seasonal minimum 6 months later. \(U_v\) should be set to between 0 and 1, and is the scaling factor at the six month minimum. The \(U(t)\) functions for different values of \(U_v\) are shown below;
Metapopulation movements
The force of infection calculation is based on the number of infected individuals
at each disease stage in each ward, \(N_s(w)\). The metapopulation
part of metawards is because individuals move between wards, and thus
will contribute to \(N_s(w)\) differently depending on when and where
they are.
The force of infection is calculated both for daytime and nighttime. Individuals contribute to the force of infection calculation for wards they visit during the daytime, and to their home ward at nighttime.
Workers visit their fixed work ward during the daytime, as long as they
are not too sick to go to work (controlled by too_sick_to_move, and
in which case they stay at home). Players
will visit a randomly chosen play ward during the daytime.
However, these movements are controlled by a cutoff parameter,
Parameters.dyn_dist_cutoff.
If the distance between the home and work ward, or home and play ward, is
greater than the cutoff (measured in kilometers), then the worker or player
will stay at home, and contribute to the force of infection of their home
ward.
Note
This is all calculated in the advance_foi()
advance function. If you want to change this, you can write your
own version of advance_foi() and set that
to be used instead via a custom iterator.
Rates of infection
The daytime and nighttime forces of infection for each ward are converted
into daytime and nighttime infection probabilities by the
advance_infprob() advance function. These give
the probability that an individual staying in the ward that day or night
would be infected. These probablities are used by the
advance_fixed() and
advance_play() advance functions to determine
whether workers or players, as they move between wards each day, would
be infected.
Enacting lockdown
Based on this knowledge, we could enact a lockdown by adjusting the
parameters used to calculate the force of infection, and the parameters
used to control movement of individuals between wards. For example,
we could reduce Population.scale_uv,
thereby reducing \(S\) in equation 1. This would have the same effect
on scaling down the FOI as scaling down \(\beta\). This would mean that
you could relate different values of \(S\) to different lockdown
control measures, e.g. closing schools, wearing masks, limiting number
of contacts etc.
We could also reduce
Parameters.dyn_dist_cutoff
to, e.g. 5 km, to prevent most work and play movements. Indeed, we could
even reduce this to 0 km to stop all movement between wards.
A good example of an alternative lockdown model is here. This is provided as an example in the MetaWards GitHub repository, and enacts lockdown by directly changing these two parameters. This has the effect of reducing the contribution from each infected individual to the overall force of infection of each ward, and reducing the movement of individuals between wards.
There are many parameters to adjust. You can also add these to your scan to investigate their impact. The full list of built-in adjustable parameters is below;
UV:
Adjust the Parameters.UV parameter
UV_max:
Adjust the Parameters.UV parameter
beta:
Adjust the Disease.beta parameter
bg_foi:
Adjust the Parameters.bg_foi parameter
contrib_foi:
Adjust the Disease.contrib_foi parameter
daily_imports:
Adjust the Parameters.daily_imports parameter
dyn_dist_cutoff:
Adjust the Parameters.dyn_dist_cutoff parameter
dyn_play_at_home:
Adjust the Parameters.dyn_play_at_home parameter
initial_inf:
Adjust the Parameters.initial_inf parameter
length_day:
Adjust the Parameters.length_day parameter
play_to_work:
Adjust the Parameters.play_to_work parameter
progress:
Adjust the Disease.progress parameter
scale_uv:
Adjust the Parameters.scale_uv parameter
static_play_at_home:
Adjust the Parameters.static_play_at_home parameter
too_ill_to_move:
Adjust the Disease.too_ill_to_move parameter
user:
Adjust a custom user-supplied parameter, held in
Parameters.user_params[name]. Set a user parameter
called 'name' via 'user.name' or '.name'.
work_to_play:
Adjust the Parameters.work_to_play parameter