Holidays and quarantine
Another use for go_ward() is to provide a good
model of the impact of individuals taking holidays to infected
destinations.
Background force of infection
We can model this by making use of the background force of infection
(bg_foi) parameter. This can be set on a per-ward basis via
Ward.bg_foi, or globally for a
network via the Parameters.bg_foi
parameters.
The background FOI is the starting value for the FOI calculation in each ward. If this is positive, then this implies that the ward has a background outbreak that will drive infections in addition to any impact on the FOI from infected individuals. If this is negative, then this implies that the ward has a background mitigation that reduces the FOI by a fixed amount regardless of the number of infected individuals (subject to the FOI not dropping below zero).
It is a constant that is added to the FOI for each ward. The global
Parameters.bg_foi is added first
to all wards, and then the per-ward
Ward.bg_foi is added for each ward.
Holiday to a different demographic
We will model the holiday destination as being a different demographic, where the global background FOI is set to a high positive value. This means that individuals who are moved to this demographic will be exposed to infection. When they then return from the holiday demographic back to their home demographic, they will carry the infection with them and then drive the epidemic back at home.
We will start by creating two demographic, home and holiday.
You can do this using Python, R, or by copying the file from below,
e.g. in Python;
>>> from metawards import Demographic, VariableSet
>>> home = Demographic("home")
>>> home.work_ratio = 1.0
>>> home.play_ratio = 1.0
>>> holiday = Demographic("holiday")
>>> holiday.work_ratio = 0.0
>>> holiday.play_ratio = 0.0
>>> adjustment = VariableSet()
>>> adjustment["scale_uv"] = 0.0
>>> adjustment["dyn_dist_cutoff"] = 0.0
>>> adjustment["bg_foi"] = 0.05
>>> holiday.adjustment = adjustment
>>> demographics = home + holiday
>>> demographics.to_json("demographics.json", indent=2, auto_bzip=False)
or in R;
> library(metawards)
> home <- metawards$Demographic("home")
> home$work_ratio <- 1.0
> home$play_ratio <- 1.0
> holiday <- metawards$Demographic("holiday")
> holiday$work_ratio <- 0.0
> holiday$play_ratio <- 0.0
> adjustment <- metawards$VariableSet()
> adjustment$set_value("scale_uv", 0.0)
> adjustment$set_value("dyn_dist_cutoff", 0.0)
> adjustment$set_value("bg_foi", 0.05)
> holiday$adjustment <- adjustment
> demographics <- metawards$Demographics()
> demographics$add(home)
> demographics$add(holiday)
> demographics$to_json("demographics.json", indent=2, auto_bzip=False)
or copy this text to the file demographics.json.
{
"demographics": ["home", "holiday"],
"work_ratios": [ 1.0, 0.0 ],
"play_ratios": [ 1.0, 0.0 ],
"adjustments": [
null,
{
"variables": {
"scale_uv": 0,
"dyn_dist_cutoff": 0,
"bg_foi": 0.05
}
}
]
}
This create home, which will start with all of the population
of the network. holiday is created as an empty network.
holiday has its parameters adjusted according to;
Parameters.scale_uvis set to zero. This stops members of theholidaydemographic from infecting each other. They will only experince the force of infection as set by the background FOI. This is realistic, as holidaymakers are unlikely to travel together in large groups, and so are unlikely to infect one another. This of course could be changed by setting scale_uv to a value above zero.Parameters.dyn_dist_cutoffis also set to zero. This stops holidaymakers from travelling outside their ward. This is because this is because they are not really in their home ward - it is used just as a marker so we can remember which ward they came from so that they can return their at the end of their holiday.Parameters.bg_foiis set to 0.05. This is a reasonable starting value for the FOI, which will drive a small outbreak infecting ~0.2% of susceptibles per day.
go_holiday and go_home
Next we will create move_holiday. Open a file called move_holiday.py
and copy in the below;
from metawards.movers import MoveGenerator, go_ward
def move_holiday(population, **kwargs):
def go_holiday(**kwargs):
gen = MoveGenerator(from_demographic="home",
to_demographic="holiday",
fraction=0.005)
go_ward(generator=gen, **kwargs)
def go_home(**kwargs):
gen = MoveGenerator(from_demographic="holiday",
to_demographic="home")
go_ward(generator=gen, **kwargs)
if population.day == 1:
return [go_holiday]
elif population.day == 14:
return [go_home]
else:
return []
This defines move_holiday. This move function returns go_holiday
on day 1 of the model, which will send individuals on holiday. It then
returns go_home on day 14 of the outbreak, which will bring
the holidaymakers back home.
Both go_holiday and go_home are simple go functions that
move individuals between the home and holiday demographics.
go_holiday moves 0.5% of the population to holiday, while
go_home brings them all back home.
We can run this model using;
metawards -d lurgy5.json -D demographics.json -m 2011Data --mover move_holiday.py --nsteps 28
Note
We are still using lurgy5.json from the last chapter, and the 2011 England
and Wales model. We have set nsteps to 28 as we are only interested
in how the epidemic spreads in the first two weeks after the
holidaymakers return.
Note
Note also that we haven’t seeded the infection. Holidaymakers picked
up the infection based only on the bg_foi of the holiday demographic.
You will see that the ~280k individuals went on holiday, with about 800 per day becoming infected;
─────────────────────────────────────────────── Day 0 ────────────────────────────────────────────────
S: 56082077 E: 0 I: 0 V: 0 R: 0 IW: 0 POPULATION: 56082077
┏━━━━━━━━━┳━━━━━━━━━━┳━━━┳━━━┳━━━┳━━━┳━━━━┳━━━━━━━━━━━━┓
┃ ┃ S ┃ E ┃ I ┃ V ┃ R ┃ IW ┃ POPULATION ┃
┡━━━━━━━━━╇━━━━━━━━━━╇━━━╇━━━╇━━━╇━━━╇━━━━╇━━━━━━━━━━━━┩
│ home │ 56082077 │ 0 │ 0 │ 0 │ 0 │ 0 │ 56082077 │
│ holiday │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │
├─────────┼──────────┼───┼───┼───┼───┼────┼────────────┤
│ total │ 56082077 │ 0 │ 0 │ 0 │ 0 │ 0 │ 56082077 │
└─────────┴──────────┴───┴───┴───┴───┴────┴────────────┘
─────────────────────────────────────────────── Day 1 ────────────────────────────────────────────────
S: 56081266 E: 811 I: 0 V: 0 R: 0 IW: 742 POPULATION: 56082077
┏━━━━━━━━━┳━━━━━━━━━━┳━━━━━┳━━━┳━━━┳━━━┳━━━━━┳━━━━━━━━━━━━┓
┃ ┃ S ┃ E ┃ I ┃ V ┃ R ┃ IW ┃ POPULATION ┃
┡━━━━━━━━━╇━━━━━━━━━━╇━━━━━╇━━━╇━━━╇━━━╇━━━━━╇━━━━━━━━━━━━┩
│ home │ 55801092 │ 0 │ 0 │ 0 │ 0 │ 0 │ 55801092 │
│ holiday │ 280174 │ 811 │ 0 │ 0 │ 0 │ 742 │ 280985 │
├─────────┼──────────┼─────┼───┼───┼───┼─────┼────────────┤
│ total │ 56081266 │ 811 │ 0 │ 0 │ 0 │ 742 │ 56082077 │
└─────────┴──────────┴─────┴───┴───┴───┴─────┴────────────┘
Number of infections: 811
─────────────────────────────────────────────── Day 2 ────────────────────────────────────────────────
S: 56080493 E: 773 I: 811 V: 0 R: 0 IW: 721 POPULATION: 56082077
┏━━━━━━━━━┳━━━━━━━━━━┳━━━━━┳━━━━━┳━━━┳━━━┳━━━━━┳━━━━━━━━━━━━┓
┃ ┃ S ┃ E ┃ I ┃ V ┃ R ┃ IW ┃ POPULATION ┃
┡━━━━━━━━━╇━━━━━━━━━━╇━━━━━╇━━━━━╇━━━╇━━━╇━━━━━╇━━━━━━━━━━━━┩
│ home │ 55801092 │ 0 │ 0 │ 0 │ 0 │ 0 │ 55801092 │
│ holiday │ 279401 │ 773 │ 811 │ 0 │ 0 │ 721 │ 280985 │
├─────────┼──────────┼─────┼─────┼───┼───┼─────┼────────────┤
│ total │ 56080493 │ 773 │ 811 │ 0 │ 0 │ 721 │ 56082077 │
└─────────┴──────────┴─────┴─────┴───┴───┴─────┴────────────┘
Number of infections: 1584
By the time they return, there are over 8000 infected holidaymakers, who spread the virus throughout the country. There is a rapid increase in the number of infected wards as the infected holidaymakers make their random (player) or fixed (worker) movements between wards;
─────────────────────────────────────────────── Day 13 ───────────────────────────────────────────────
S: 56072036 E: 718 I: 5657 V: 0 R: 3666 IW: 662 POPULATION: 56082077
┏━━━━━━━━━┳━━━━━━━━━━┳━━━━━┳━━━━━━┳━━━┳━━━━━━┳━━━━━┳━━━━━━━━━━━━┓
┃ ┃ S ┃ E ┃ I ┃ V ┃ R ┃ IW ┃ POPULATION ┃
┡━━━━━━━━━╇━━━━━━━━━━╇━━━━━╇━━━━━━╇━━━╇━━━━━━╇━━━━━╇━━━━━━━━━━━━┩
│ home │ 55801092 │ 0 │ 0 │ 0 │ 0 │ 0 │ 55801092 │
│ holiday │ 270944 │ 718 │ 5657 │ 0 │ 3666 │ 662 │ 280985 │
├─────────┼──────────┼─────┼──────┼───┼──────┼─────┼────────────┤
│ total │ 56072036 │ 718 │ 5657 │ 0 │ 3666 │ 662 │ 56082077 │
└─────────┴──────────┴─────┴──────┴───┴──────┴─────┴────────────┘
Number of infections: 6375
─────────────────────────────────────────────── Day 14 ───────────────────────────────────────────────
S: 56069022 E: 3014 I: 5727 V: 0 R: 4314 IW: 2396 POPULATION: 56082077
┏━━━━━━━━━┳━━━━━━━━━━┳━━━━━━┳━━━━━━┳━━━┳━━━━━━┳━━━━━━┳━━━━━━━━━━━━┓
┃ ┃ S ┃ E ┃ I ┃ V ┃ R ┃ IW ┃ POPULATION ┃
┡━━━━━━━━━╇━━━━━━━━━━╇━━━━━━╇━━━━━━╇━━━╇━━━━━━╇━━━━━━╇━━━━━━━━━━━━┩
│ home │ 56069022 │ 3014 │ 5727 │ 0 │ 4314 │ 2396 │ 56082077 │
│ holiday │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │
├─────────┼──────────┼──────┼──────┼───┼──────┼──────┼────────────┤
│ total │ 56069022 │ 3014 │ 5727 │ 0 │ 4314 │ 2396 │ 56082077 │
└─────────┴──────────┴──────┴──────┴───┴──────┴──────┴────────────┘
Number of infections: 8741
─────────────────────────────────────────────── Day 15 ───────────────────────────────────────────────
S: 56065953 E: 3069 I: 8059 V: 0 R: 4996 IW: 2389 POPULATION: 56082077
┏━━━━━━━━━┳━━━━━━━━━━┳━━━━━━┳━━━━━━┳━━━┳━━━━━━┳━━━━━━┳━━━━━━━━━━━━┓
┃ ┃ S ┃ E ┃ I ┃ V ┃ R ┃ IW ┃ POPULATION ┃
┡━━━━━━━━━╇━━━━━━━━━━╇━━━━━━╇━━━━━━╇━━━╇━━━━━━╇━━━━━━╇━━━━━━━━━━━━┩
│ home │ 56065953 │ 3069 │ 8059 │ 0 │ 4996 │ 2389 │ 56082077 │
│ holiday │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │
├─────────┼──────────┼──────┼──────┼───┼──────┼──────┼────────────┤
│ total │ 56065953 │ 3069 │ 8059 │ 0 │ 4996 │ 2389 │ 56082077 │
└─────────┴──────────┴──────┴──────┴───┴──────┴──────┴────────────┘
Number of infections: 11128
The outbreak grows rapidly, until by day 28 there have been over 300k infections;
─────────────────────────────────────────────── Day 28 ───────────────────────────────────────────────
S: 55768352 E: 65734 I: 194526 V: 0 R: 53465 IW: 8454 POPULATION: 56082077
┏━━━━━━━━━┳━━━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━┳━━━━━━━┳━━━━━━┳━━━━━━━━━━━━┓
┃ ┃ S ┃ E ┃ I ┃ V ┃ R ┃ IW ┃ POPULATION ┃
┡━━━━━━━━━╇━━━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━╇━━━━━━━╇━━━━━━╇━━━━━━━━━━━━┩
│ home │ 55768352 │ 65734 │ 194526 │ 0 │ 53465 │ 8454 │ 56082077 │
│ holiday │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │ 0 │
├─────────┼──────────┼───────┼────────┼───┼───────┼──────┼────────────┤
│ total │ 55768352 │ 65734 │ 194526 │ 0 │ 53465 │ 8454 │ 56082077 │
└─────────┴──────────┴───────┴────────┴───┴───────┴──────┴────────────┘
Number of infections: 260260
Modelling quarantine
One method of preventing holidaymakers from spreading the infection when
they return home is to require them all to enter quarantine. We can
model this by creating a third, quarantine demographic. You can
do this in python by typing;
>>> from metawards import Demographic, VariableSet
>>> home = Demographic("home")
>>> home.work_ratio = 1.0
>>> home.play_ratio = 1.0
>>> holiday = Demographic("holiday")
>>> holiday.work_ratio = 0.0
>>> holiday.play_ratio = 0.0
>>> adjustment = VariableSet()
>>> adjustment["scale_uv"] = 0.0
>>> adjustment["dyn_dist_cutoff"] = 0.0
>>> adjustment["bg_foi"] = 0.05
>>> holiday.adjustment = adjustment
>>> quarantine = Demographic("quarantine")
>>> quarantine.work_ratio = 0.0
>>> quarantine.play_ratio = 0.0
>>> adjustment = VariableSet()
>>> adjustment["scale_uv"] = 0.0
>>> adjustment["dyn_dist_cutoff"] = 0.0
>>> quarantine.adjustment = adjustment
>>> demographics = home + holiday + quarantine
>>> demographics.to_json("demographics.json", indent=2, auto_bzip=False)
or in R;
> library(metawards)
> home <- metawards$Demographic("home")
> home$work_ratio <- 1.0
> home$play_ratio <- 1.0
> holiday <- metawards$Demographic("holiday")
> holiday$work_ratio <- 0.0
> holiday$play_ratio <- 0.0
> adjustment <- metawards$VariableSet()
> adjustment$set_value("scale_uv", 0.0)
> adjustment$set_value("dyn_dist_cutoff", 0.0)
> adjustment$set_value("bg_foi", 0.05)
> holiday$adjustment <- adjustment
> quarantine <- metawards$Demographic("quarantine")
> quarantine$work_ratio <- 0.0
> quarantine$play_ratio <- 0.0
> adjustment <- metawards$VariableSet()
> adjustment$set_value("scale_uv", 0.0)
> adjustment$set_value("dyn_dist_cutoff", 0.0)
> quarantine$adjustment <- adjustment
> demographics <- metawards$Demographics()
> demographics$add(home)
> demographics$add(holiday)
> demographics$add(quarantine)
> demographics$to_json("demographics.json", indent=2, auto_bzip=False)
or copy this text to the file demographics.json.
{
"demographics": ["home", "holiday", "quarantine"],
"work_ratios": [ 1.0, 0.0, 0.0 ],
"play_ratios": [ 1.0, 0.0, 0.0 ],
"adjustments": [
null,
{
"variables": {
"scale_uv": 0,
"dyn_dist_cutoff": 0,
"bg_foi": 0.05
}
},
{
"variables": {
"scale_uv": 0,
"dyn_dist_cutoff": 0
}
}
]
}
The qurantine demographic has both
Parameters.scale_uv and
Parameters.dyn_dist_cutoff
as zero, just like the holiday demographic, because holidaymakers
should be self-isolating and thus not infecting one another. The
Parameters.bg_foi parameter is
not set, meaning that it keeps its default value of zero, meaning that
there is no background driver for more infections.
go_quarantine
We now need to write a go_quarantine function and add it to
move_holiday. Edit move_holiday.py and copy in the below;
from metawards.movers import MoveGenerator, go_ward
def move_holiday(population, **kwargs):
def go_holiday(**kwargs):
gen = MoveGenerator(from_demographic="home",
to_demographic="holiday",
fraction=0.005)
go_ward(generator=gen, **kwargs)
def go_quarantine(**kwargs):
gen = MoveGenerator(from_demographic="holiday",
to_demographic="quarantine")
go_ward(generator=gen, **kwargs)
def go_home(**kwargs):
gen = MoveGenerator(from_demographic="quarantine",
to_demographic="home")
go_ward(generator=gen, **kwargs)
holiday_length = 14
quarantine_length = 14
if population.day == 1:
return [go_holiday]
elif population.day == holiday_length:
return [go_quarantine]
elif population.day == holiday_length+quarantine_length:
return [go_home]
else:
return []
Here we have changed go_holiday so that individuals go to
quarantine instead of home. We have then added go_quarantine
that moves all individuals from quarantine to home.
We’ve then set move_holiday to return go_quarantine at the
end of their 14-day holiday, and then return go_home at the end
of the 14-day quarantine.
We can run this using;
metawards -d lurgy5.json -D demographics.json -m 2011Data --mover move_holiday.py --nsteps 48
and then plot using
metawards-plot -i output/results.csv.bz2
What I see is that the 14 days of quarantine is not quite long enough for the lurgy. There are still ~400 infections, which drive a further 300 infections when the holidaymakers leave quarantine. This can be see in the infection graphs, e.g.
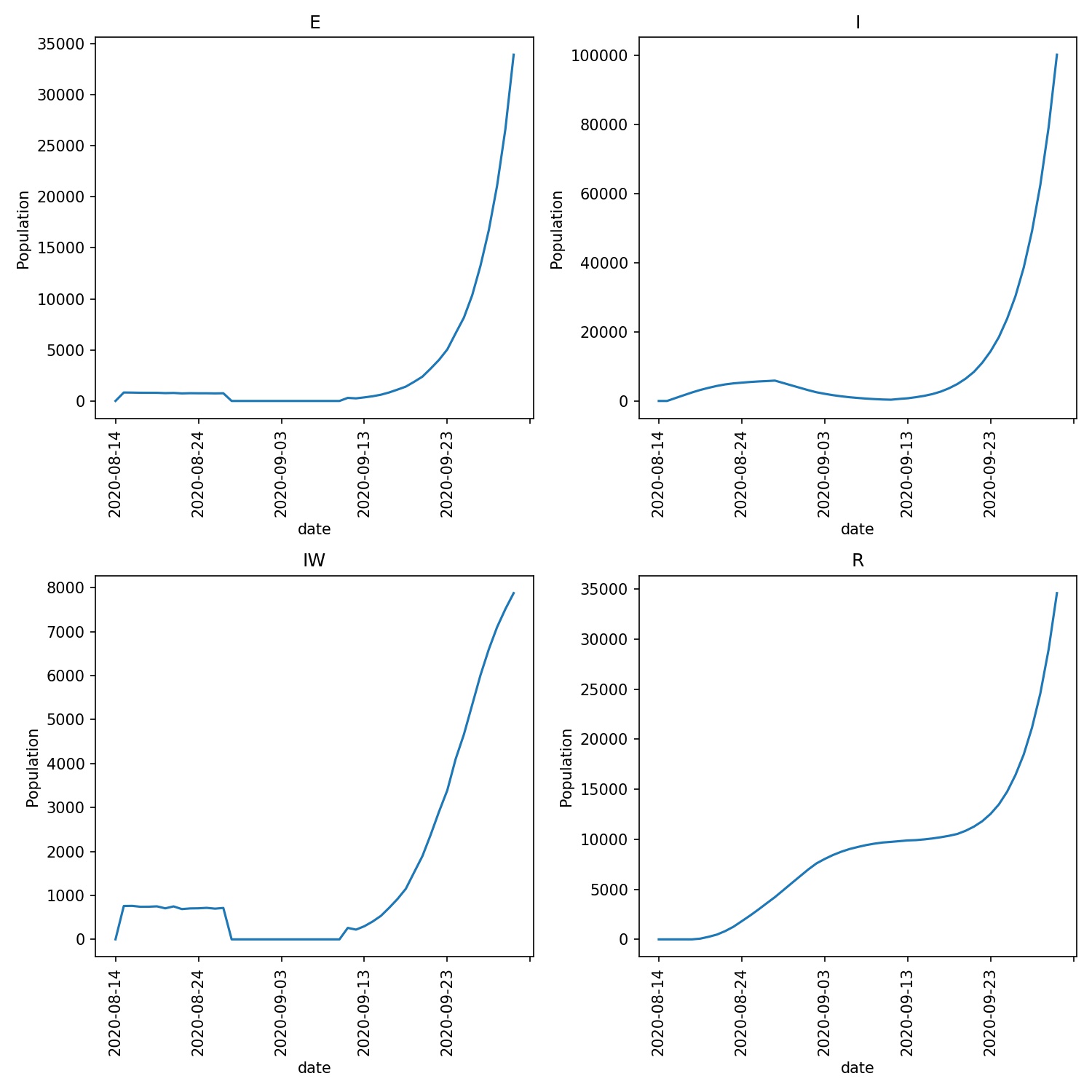
What next?
You could extend the above model in many ways;
You could model different lengths of quarantine by setting quarantine_length via a custom user parameter, and then scanning it to see the impact on the outbreak.
You could model different holiday destinations with different background FOIs, to see how you could classify destinations according to the risk they pose to home.
You could model different levels of compliance with quarantine by having a fraction of holidaymakers go straight home (set
fractionto a value less than one ingo_quarantineand have the remaindergo_home).You could model quarantine fatigue, similarly to how you modelled self-isolation fatigue in part 6.
You could model the impact of holidaymakers during different stages in an outbreak at home, by seeding the outbreak at home, and then having the holiday start later in the year.
You could model the impact of different lockdown measures at home, and see how they are disrupted by holidaymakers returning from holiday.
Note
Congratulations on reaching the end of the tutorial. Hopefully this
has given you a good insight into what you could do with metawards.
If you have any questions then please
post an issue to our GitHub repository.
Please feel free to post issues to request more tutorials, or to
ask for more documentation.
Note
If you are moving on to developing metawards, or writing more
complex code on top of metawards, then you should read the
developer documentation for the metawards module, which can be
found here.